CS502 Assignment #1 Solution 2019
__________
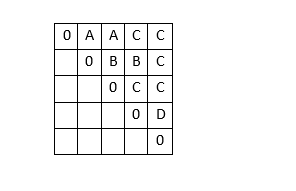
Repeat process diagonal the number of possible splits values of k increases:
That leaves the m [A, E] which can now be computed:
Based on the computation, the minimum cost for the multiplying the five matrices is 78 and the
B. How many cycles are there in the given directed graph, list all of
CS502 Assignment
Solution 2019
Q#1) Consider the following five matrices A, B, C, D and E
along their
dimensions;
A B C
D E
(6x5)
(5x1) (1x7) (7x4) (4x2)
Determine the Optimal Multiplication Order for the above
matrices
using Dynamic Programing approach and also present the
sequence
(i.e. optimal order) in binary tree.
Solution: -
Second super diagonal this time, however, we will need to
try two possible values for k. for
example, there are two possible splits for computing m [A,
C]; we will choose the split that
Occurs with K=1
Repeat process diagonal the number of possible splits values of k increases:
That leaves the m [A, E] which can now be computed:
Based on the computation, the minimum cost for the multiplying the five matrices is 78 and the
optimal order for multiplication is
((A(BC)) (DE))
Q#2) CS502 Assignment 1 solution 2019
A. List down in and Out Degree of vertices of the given
directed
graph.
Solution:
B. How many cycles are there in the given directed graph, list all of
them. Further, is there any Hamiltonian cycle in it(yes/no)?
Answer: -
There are five
cycles in the given directed graph.
______________________________________
_____________________________________


















Post a Comment